在三角形abc中 角a b c的对边分别为abc...(数学正弦定理的解题方法)
• y35******5 • 2015-01-14 •
有学生问小编一道关于数学正弦定理的数学题,题目如下:在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b﹣c)cosA﹣acosC=0,(Ⅰ)求角A的大小;(Ⅱ)若,,试判断△ABC的形状,并说明理由.那么关于这样的 ...
有学生问小编一道关于数学正弦定理的数学题,题目如下:
在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b﹣c)cosA﹣acosC=0,
(Ⅰ)求角A的大小;
(Ⅱ)若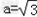 ,
,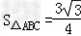 ,试判断△ABC的形状,并说明理由.
,试判断△ABC的形状,并说明理由.
那么关于这样的正弦的题,可以怎么处理呢?看看21教育名师怎么解这个题目吧:
解:(Ⅰ)∵(2b﹣c)cosA﹣acosC=0,由正弦定理,
得(2sinB﹣sinC)cosA﹣sinAcosC=0,
∴2sinBcosA﹣sin(A+C)=0,sinB(2cosA﹣1)=0,
∵0<B<π,
∴sinB≠0,
∴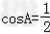 ,
,
∵0<A<π,
∴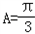 ..
..
(Ⅱ)∵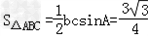 ,
,
即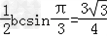
∴bc=3①
由余弦定理可知cosA=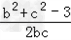 =
=
∴b2+c2=6,②
由①②得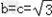 ,
,
∴△ABC为等边三角形.
在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b﹣c)cosA﹣acosC=0,
(Ⅰ)求角A的大小;
(Ⅱ)若
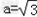 ,
,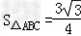 ,试判断△ABC的形状,并说明理由.
,试判断△ABC的形状,并说明理由.那么关于这样的正弦的题,可以怎么处理呢?看看21教育名师怎么解这个题目吧:
解:(Ⅰ)∵(2b﹣c)cosA﹣acosC=0,由正弦定理,
得(2sinB﹣sinC)cosA﹣sinAcosC=0,
∴2sinBcosA﹣sin(A+C)=0,sinB(2cosA﹣1)=0,
∵0<B<π,
∴sinB≠0,
∴
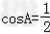 ,
,∵0<A<π,
∴
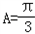 ..
..(Ⅱ)∵
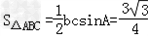 ,
,即
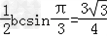
∴bc=3①
由余弦定理可知cosA=
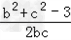 =
=
∴b2+c2=6,②
由①②得
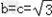 ,
,∴△ABC为等边三角形.
声明:该文由入驻作者投稿,内容仅供参考,不构成任何投资建议,如果内容侵犯了您的权利,请通知站长处理
