听课，听同行讲课，只要是老师都会经历，它是老师们相互学习、交流的重要途径。多年来，无论是在学校做老师还是在教育行政管理部门做教学研究和教育管理工作，听课是必须的。然每次听老师们的课，总有种忐忑的心情，总有一种莫名的担心。听胡柳军老师讲课之前却很平静，与老胡共事多年，其知识功底之扎实、教学经验之丰富、课堂应变之纯熟，自愧不如。听其讲课就像观看老艺术家的表演---欣赏。倒是临听课的时候尴尬了----我迟到了几秒钟。
    老胡今天讲《空间直线与直线之间的位置关系》，目标：正确理解异面直线的定义；会判断空间两条直线的位置关系；掌握平行公理及空间等角定理的内容和应用；会求异面直线所成角的大小。目标明确，40分钟的教与学，行如流水，师生在和谐、愉快的双向交交流中顺利实现了目标。 老胡今天的课给我印象深刻的首先是教学过程中出现的几个“意外”： 意外之一:讲空间等角定理 时,老师准备的课件里只动画显示“两个角的两边分别对应平行这两个角相等”的情况，(为什么只显示一种？是故意还是疏忽？我认为是前者), 因为初中平面几何有类似的结论，“如果两个角的两边分别对应平行，那么这两个角相等或互补”，而在空间通过实物的展示和学生的思考、类比得出了定理 “空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。”是“意外” 也是“意料之中” ？这是智慧。

     意外之二：讲例1 ，实际是让学生做 。如图, E、F、G、H分别为空间四边形ABCD 各边 的中点，求证：四边形EFGH为平行四边形。两个学生到台前演排, 一个学生做对了, －个做错了, 后者的作题过程毫无可取之处。这应该是－个真正的意外，老师没有责难, 没有批评, 在给予简单客观的评价后，给错者一个宽容的微笑。这是情怀。
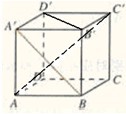
    意外之三: 练习: 在正方体 中，求异面直线 与 所成的角.这个题有点难度, 有学生通过平移后知道∠A’C’B是异面直线 与 所成角的平面角. 但说其大小是90度, 因为∠A’C’B’ 与∠BC’B’ 都是45度. 老师提问: “∠A’C’B’ 与∠BC’B’ 在同一平面内吗？”学生们马上意识到∠A’C’B不是90度.学生出现这样的“意外”,N年出现过N次, 早知道该怎么应对（空间的两个角是不能象平面内的角求和）。这是经验。

     意外之四：续三之练习，∠A’C’B的大小是多少呢？大部分同学都在积极的思考和讨论，有的同学甚至站起来表达自己的意见。老师－边倾听学生的表述, －边象一名老猎手在等待猎物的出现, 更像达. 芬奇在捕捉蒙娜丽莎的笑容。机会来了，一位坐着的同学轻声的说：“连结A’B”. 老师马上请这位同学讲述自己的想法，得出异面直线 与 所成的角为60度. 同学们的脸上写满了开心的表情，老胡本来就不大的眼睛眯成了一条线。这是敏锐。
    教学中常常出现“意外”， 这“意外” 是意料之中还是意料之外？两者都应有，都会有。能灵活、机智、适度的把握和处理好“意外”， 就能使“意外” 有意外的收获。
    另外老胡今天的课有个地方有点“乱”:
    如图，在正方体中，求下列异面直线所成的角。
    ⑴ BA'和CC' ⑵ B'D'和 AC

     动手试试: 在正方体ABCD-A'B'C'D' 中，求异面直线 AC与BC' 所成的角。
     因为三个问题集中在同一个图形上，在“动手试试”时图形中的线条就多了起来，老师也自言有点“乱”了。我在听课记录上写道: “把一个图改成三个图就可以解决‘乱’ 的问题”（其实老师在电子白板上用红色显示了第3个问题中的线段，解决了“乱”） 。下课后突然想起毛泽东的《湖南农民运动考察报告》，觉得老胡这“乱” ，“乱”得好，我们不正是要培养孩子们从复杂的线条中寻找有效线条，在复杂的问题中学会准确判断的能力么？
     品味老胡的40分钟，课堂构建匠心独到，内容丰富，是师生探究新知的桥梁；教学过程若潺潺流水，沁人心肺；师生互动心情舒畅，慈父童心；这“意外” 就如那小溪中的几朵美丽的浪花；至于那点“乱” 就是母鸡领着一群小鸡在悠闲的寻寻觅觅。
好一幅大师的画作-----小桥流水人家。
    从事教育工作30多年，听过多少课没有准确的统计，但每次听课总会有一些“意外”的收获。